Sensitivity and Specificity

Often when reading peer-reviewed articles I feel like I need an advanced degree in statistics to understand how the hell they analyzed the information and quantified the results.  There is an amazing amount of jargon when looking at the objective measurements.  This is rarely a clinical problem since understanding the statistical analysis is not applicable to the patient.  I’ve never been mobilizing a patients shoulder and been concerned of whether it was a pearsons analysis or t-something in the article I just read.

However, the one part of statistics that is very important clinically is understanding specificity and sensitivity.  Sensitivity and Specificity are used to discriminate relevant information that allows clinicians to make meaningful decisions.  They are a statistical measurement for a classification function.  Using sensitivity and specificity can allow clinicians to improve their examination, optimize their assessment, clear up any suspicions, and most importantly, lead clinicians to the proper interventions and prevent patients from receiving unnecessary treatment.

So what’s the problem then?  Unfortunately, due to poor explanations, difficult concepts, and confusion among peers they often become used interchangeably.   For the quick explanation scroll down to the chart at the bottom of this post.

Statistical Example

To attain these statistical values, studies have to be performed on the accuracy of a test against the current gold standard.  Here’s an example of a possible test to determine the sensitivity and a specificity of the Lachmans test (completely fictional).

If 100 patients known to have an ACL tear were tested with the Lachman’s test, and 90 of them tested positive, then the Lachman’s test would have a 90% sensitivity.  If 100 patients known to have an intact ACL were tested with the Lachman’s test, and 90 of them tested negative, then the test would have a 90% specificity.

Sensitivity

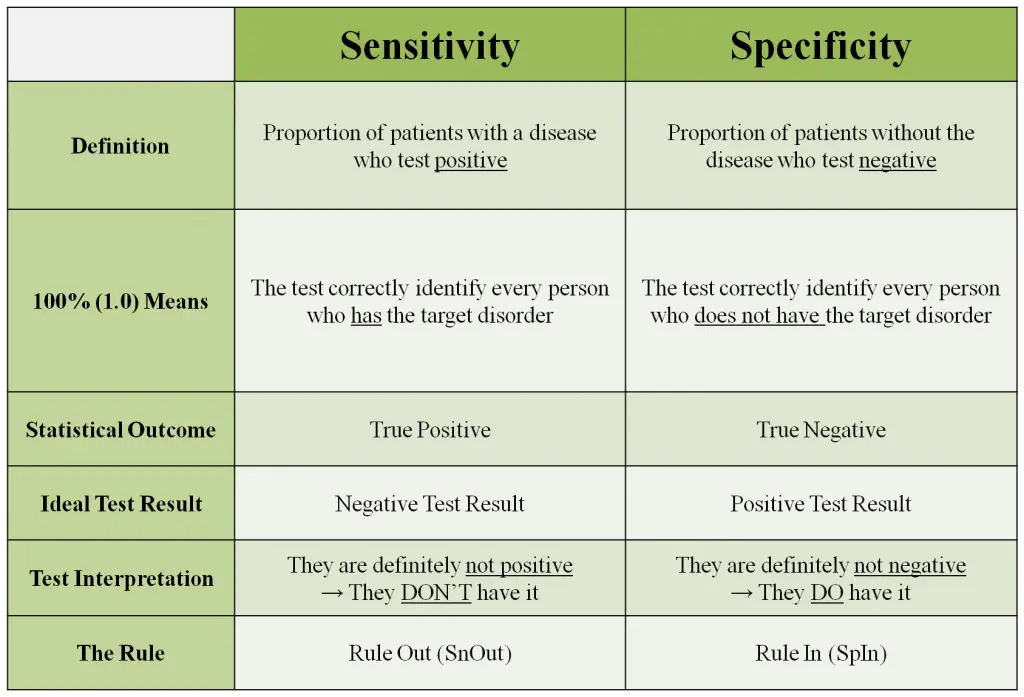
Sensitivity can be defined as the proportion of patients with a pathology who test positive.  It relates to the test’s ability to identify positive results.   A test that has a sensitivity of 1.0 would be able to correctly diagnose every person who has the target pathology (predicts all people from the sick group as sick).  A highly sensitive test implies that it has the ability to identify the patient who actually has the pathology.  In other words, sensitivity determines the amount of true positive outcomes.

Since a highly sensitive test would identify anyone that tested positive for the pathology, then someone who tested negative could be ruled out for the pathology.  This is because if they were positive, it would have been proven with the test.  Therefore for a negative result would confirm that the patient does NOT have the pathology.  This is where the “SnOut” rule comes in.  Because a negative response to a high sensitive test rules out the pathology.

In terms of statistics and errors, you could say that if it is a true positive, then it is not going to be a false negative.  A 100% true positive would mean there is no type II error.  There is no false negative.  A negative result would be considered valid and not an error.

Clinically Application

Sensitivity tests are used to screen for pathologies.  An upper or lower quarter screen isn’t used to try to rule anything in.  Instead it is used to rule out any possible pathologies.  It’s why many use the term “clearing” the upper/lower quarter.  The FMS is also a sensitive screening test.  On the functional movement’s you are not analyzing and testing for a certain pathology, you’re simply ruling out the individuals who are not at risk.  By doing so it allows you to identify which individuals need to be evaluated more in depth.

Another example of the clinical application of sensitive tests would be with shoulder pathologies.  I have found clinically that most acute shoulders test positive for just about every special test.  This may be due to the acute irritation of the joint and increased sensitivity to pain, which is often the positive sign.  Therefore, it might be better to use tests with high sensitivity in this acute stage in attempt to rule out what pathology the patient does not have.

Real Life Example

Think of tequilla.  The past couple times you’ve taken shots of tequilla it has ALWAYS ended up with you not feeling so well.  You are positive that no matter how many limes you chase it with, you are definitely going to be feeling bad if you drink tequilla.  And when you don’t have tequilla you feel fine and don’t get sick at all.  So when you’re at the bar ordering something to drink what do you NOT order?  What drink do you immediately rule out?  Tequilla.  You know tequilla will definitely make you sick and not having it will leave you feeling good.  So you can “SnOut” tequilla.

So in this spring break example, Tequilla would have a 100% sensitivity to you.  You are positive you’ll get sick off of it if you have it.  So when the bartender does his test of asking you what you want to drink, you give him a confident negative result that you don’t have tequilla.

Specificity

Specificity can be defined as the proportion of patients without the disease who test negative.  A test with 1.0 specificity would be able to correctly identify every person who does not have the target disorder (not predict anyone from the health group as sick).  A test with high specificity would be able to determine the population that does not have the pathology.  Specificity shows the true negatives.

As mentioned above in sensitivity, it is a process of elimination between two options.  Because of this binary classification, the results are directly proportional.  Since a highly specific test would definitely display the absence of the pathology, then if the patient test positive, you can be certain that they actually have it.  Therefore, a positive test result rules in the target disorder (“SpIn”).

In terms of statistics and errors, you could say that if it is a true negative, then it is not going to be a false positive.  A 100% true negative would mean there is no type I error.  There is no false positive.  A positive result would be considered valid and not an error.

Clinical Application

Specific tests are used for rule in a pathology that a clinician may be suspicious of.  For example, if during your examination you become suspicious that your patient may have a meniscus tear.  Sure you could use a sensitive test such as joint line tenderness to rule it out, but if all signs and symptoms are leading to a meniscus tear, then you really want to use a specific test to rule it in.  The Apley’s test has been shown to have a high specificity.  If this test is negative, then it would be logical to use a sensitive test to further rule it out.  For further confidence in test results, using a test with both high specificity and sensitivity (e.g. Thessaly test) would be ideal.

Real Life Example

Staying with the alcohol example of ordering a drink at a bar, think of that tasty micro brew on tap.  Everytime you have that tasty beer you have a great time and have never been sick off of it.  It never has a negative effect on you.  You are certain that it will go great with those mozarella sticks and nacho’s you just ordered.  So when the bartender asks you what you want to drink what do you rule in?  What are you positive that you want to drink?  The micro brew beer, especially if it’s 2 for 1.  So you can “SpIn” beer.

So in this happy hour example, beer is 100% specific to you.  You are certain that beer will not make you sick.  So when the bartender tests you by asking you what do you want to drink, you give him a confident positive result that you want to order a beer.

Summary

If the application of specificity and sensitivity seems backwards, it’s because it is.  This is the fun world of statistical analysis, binary classification function, and errors associated with the null hypothesis.

• A high sensitive test would definitely catch anyone that is positive.  So if they’re not positive, you can be sure that they’re negative.
• A high specificity test would definitely catch anyone that is negative.  So if they’re not negative, you can be sure that they’re positive.

The general rule for a good test value is approximately 80%.

Chart of Sensitivity and Specificity

 

Bottom Line

Sensitivity and specificity are great values to guide you in your clinical examination.  It can give more information regarding the patient and lead to a better assessment and a more valid diagnosis.  Keep in mind that there is always the possibility of false positives and negatives.  Special tests should never be the only sign to determine a patients pathology.  It is merely a piece of the clinical examination and assessment.

References

Dutton M.   Orthopaedic Examination, Evaluation, & Intervention.  New York: McGraw-Hill; 2004.

Magee DJ.  Orthopedic Physical Assessment (5th ed.).  St. Louis: Saunders; 2008.

 
 
—

The main reason I do this blog is to share knowledge and to help people become better clinicians/coaches. I want our profession to grow and for our patients to have better outcomes. Regardless of your specific title (PT, Chiro, Trainer, Coach, etc.), we all have the same goal of trying to empower people to fix their problems through movement. I hope the content of this website helps you in doing so.

If you enjoyed it and found it helpful, please share it with your peers. And if you are feeling generous, please make a donation to help me run this website. Any amount you can afford is greatly appreciated.

 

Leave This Blank:Leave This Blank Too:Do Not Change This:

Your email: